Strong, fast, non-cryptographic 32/64 hash function
Zedmee is based on the use of a table of random numbers; the algorithm is minimalist and uses only bitwise, shift and adding operations.
The table contains 256 ramdom values (one for each byte); by default zedmee uses a table generated with the LFSR113 algorithm for the 32-bit version or LFSR258 for the 64 bit version, but any other random table can be used; it is also possible to specify a seed.
The result may seem like a trivial algorithm, as a multiplicative hash function, but the characteristics and quality of the result are equal to if not superior to the best and complex hash functions.
public static int hash(final byte[] data, int pos, int length, int seed, final int[] table) {
int h = seed;
while(length > 0)
h = table[(--length + data[pos + length]) & 0xFF] ^ ((h << 2) + h);
return h;
}Zedmee has an absolutely uniform, chaotic distribution of hash values independent of the number, length and type of input values.
It also has a good Avalanche Effect property: even a minimal differences (1 bit) of input values produces very different hash values.
Zedmee produces a very low number of collisions for each reasonably large number of distinct values; it is close to the collisions number of a Universal Hash Function.
The number is given by the formula n-m*(1-((m-1)/m)^n) where n is the number of input values, m is the number of all possible hash values (2^32 or 2^64).
| Data input | #Values | #Expected Collisions | Zedmee | Murmur3 | XX |
|---|---|---|---|---|---|
| 4-bytes values 00000000-05F5E0FF | 100,000,000 | 1,155,170 | 1,152,721 | 0 | 0 |
| 4-bytes values FA0A1F00-FFFFFFFF | 100,000,000 | 1,155,170 | 1,154,388 | 0 | 0 |
| 1 to 3 bytes values 00-FF, 0100-FFFF, 010000-FFFFFF | 16,777,216 | 32,725 | 32,358 | 0 | 0 |
| 1 to 3 bytes values 00-FF, 0000-FFFF, 000000-FFFFFF | 16,843,008 | 32,982 | 32,606 | 0 | 0 |
Note: both Murmur and XX for arrays up to 4 bytes long (8 for version 64) behave like perfect hash functions (0 collisions), but this feature makes them more vulnerable.
| Data input | #Vaues | #Expected Collisions | Zedmee | Murmur3 | XX |
|---|---|---|---|---|---|
| Numbers as strings from "0" to "999999999" | 1,000,000,000 | 107,882,641 | 107,869,763 | 107,822,463 | 110,287,893 |
| File words_en.txt | 65,503 | 0 | 0 | 0 | 0 |
| File words_es.txt | 74,571 | 0 | 0 | 2 | 0 |
| File words_it.txt | 117,558 | 1 | 0 | 0 | 2 |
| File words_latin.txt | 80,007 | 0 | 0 | 1 | 1 |
| File words_en_es_it_latin.txt | 315,198 | 11 | 8 | 9 | 9 |
| File words_and_numbers.txt | 429,187 | 21 | 14 | 20 | 19 |
| File first_million_primes.txt | 1,000,000 | 116 | 101 | 118 | 85 |
| File random_64bit_signed_nums.txt | 1,000,000 | 116 | 101 | 110 | 143 |
| File rockyou.txt dictionary of common passwords | 14,442,069 | 24,254 | 168,230 | 168,887 | 168,563 |
32-bit: number of collisions for data input from [19-48] bytes. 100,000,000 values, 1,155,170 expected collisions
| Data input | Zedmee | Murmur3 | XX |
|---|---|---|---|
| Number as strings from "1234567890123456789" to "1234567890223456788" | 1,152,279 | 1,155,789 | 808,693 |
| Strings from "abcdefg1234567890123456789hijklmn" to "abcdefg1234567890223456788hijklmn" | 1,153,907 | 1,152,600 | 1,037,151 |
| Binary 24 bytes [b,b,b,b,b,b], b from 00000000 to 05F5E0FF | 1,155,010 | 1,154,653 | 1,411,483 |
| Binary 24 bytes [b,b*3,b*5,b*7,b*11,b*13], b from 00000000 to 05F5E0FF | 1,155,521 | 1,154,542 | 1,160,003 |
| Strings 48 length "ssssss", s from "00000000" to "05F5E0FF" | 1,154,055 | 1,156,254 | 1,155,854 |
| Random 32 bytes [rrrrrrrr], r from 00000000 to FFFFFFFF random | 1,154,774 | 1,156,450 | 1,154,307 |
64-bit: number of collisions for data input string "sssss", s from "000000000" to "2540BE3FF". 10,000,000,000 values
| Function | #Collisions | Values |
|---|---|---|
| Zedmee | 2 | Collision: F0 BA CA 4A 12 C3 05 42 Strings: "17508DC8A17508DC8A17508DC8A17508DC8A17508DC8A", "1E840E8311E840E8311E840E8311E840E8311E840E831" |
| Collision: A3 66 AE B1 81 F5 D8 82 Strings: "06C1D96E206C1D96E206C1D96E206C1D96E206C1D96E2", "0A00D74120A00D74120A00D74120A00D74120A00D7412" |
||
| Murmur3 | 5 | Collision: 45 F0 06 CF E1 6F F4 D7 Strings: "07AF2BABB07AF2BABB07AF2BABB07AF2BABB07AF2BABB", "184D0B97E184D0B97E184D0B97E184D0B97E184D0B97E" |
| Collision: 88 B9 B4 F8 9A EF 0B 0D Strings: "1C60B95911C60B95911C60B95911C60B95911C60B9591", "1F3A5D9AE1F3A5D9AE1F3A5D9AE1F3A5D9AE1F3A5D9AE" |
||
| Collision: B1 B2 60 25 7D 9C DF 95 Strings: "0E152D31E0E152D31E0E152D31E0E152D31E0E152D31E", "181B53CCC181B53CCC181B53CCC181B53CCC181B53CCC" |
||
| Collision: D3 ED E1 23 5C 9A 41 D4 Strings: "05C06C20B05C06C20B05C06C20B05C06C20B05C06C20B", "131D7411C131D7411C131D7411C131D7411C131D7411C" |
||
| Collision: EA 2F 63 5A 7B 41 EF 22 Strings: "1A89ECD471A89ECD471A89ECD471A89ECD471A89ECD47", "24F1BB43A24F1BB43A24F1BB43A24F1BB43A24F1BB43A" |
||
| XXHash | 3 | Collision: 73 5A C8 30 AC 14 DA 27 Strings: "101570C93101570C93101570C93101570C93101570C93", "17F255DF617F255DF617F255DF617F255DF617F255DF6" |
| Collision: 7E 7B E5 32 95 6E CC C8 Strings: "05652E7A205652E7A205652E7A205652E7A205652E7A2", "179BFA274179BFA274179BFA274179BFA274179BFA274" |
||
| Collision: C3 DC 2E 55 5B F3 82 A0 Strings: "003AA63E8003AA63E8003AA63E8003AA63E8003AA63E8", "1AB1E788D1AB1E788D1AB1E788D1AB1E788D1AB1E788D" |
64-bit: number of collisions for data input string from "0000000000000000000000000000000000000000000000000000000000000000" to "0000000000000000000000000000001001010100000010111110001111111111". 10,000,000,000 values
| Function | #Collisions | Values |
|---|---|---|
| Zedmee | 0 | |
| Murmur3 | 4 | Collision: 0B 55 34 BF 60 C9 18 61 Strings: "0000000000000000000000000000000100001001010101111010111010000111" "0000000000000000000000000000000101011101001010100101010000100010" |
| Collision: 12 A1 E3 16 DE E8 3F BD Strings: "0000000000000000000000000000000001000010110011100001100100100001" "0000000000000000000000000000000101000001111110010000010100010001" |
||
| Collision: BD 82 F1 B3 16 97 8B 9B Strings: "0000000000000000000000000000000101111010100110011011010000110110" "0000000000000000000000000000000111110111000001011000101000010111" |
||
| Collision: C0 43 69 54 EB C9 3C 71 Strings: "0000000000000000000000000000000000010100111100101000100100011110" "0000000000000000000000000000000111101011101100110110101011010010" |
||
| XXHash | 5 | Collision: 5E 60 EB 72 92 CC BB 25 Strings: "0000000000000000000000000000000001110100111100100000100000001100" "0000000000000000000000000000000101101111010000001011011000110100" |
| Collision: 60 5F 66 6F 5A 60 67 99 Strings: "0000000000000000000000000000000100001010011000010000100100100011" "0000000000000000000000000000000101010101111100111010110000111110" |
||
| Collision: 8E 7E 33 FF B8 0E 68 85 Strings: "0000000000000000000000000000000100010101010100101011000000001101" "0000000000000000000000000000000101100110001000111010101100111101" |
||
| Collision: FA DC A0 70 68 5E B3 3B Strings: "0000000000000000000000000000000100110110000101111100101101101100" "0000000000000000000000000000000111111010100100000001101011001110" |
||
| Collision: 36 E1 36 72 81 90 A7 B9 Strings: "0000000000000000000000000000000101010100000000010101000111110000" "0000000000000000000000000000001000010110110000101010001111011011" |
Note: Since murmur3 implements only 32 or 128-bit functions, the first 8 bytes of the 128-bit hash were used to obtain 64-bit hash, as suggested by the author
If you first know that the input values are limited to a subset of all possible bytes, e.g. alphanumeric strings, printable ascii, digit only... you can use a special table to minimize collisions with that particular input subset. A simple statistical program can be used to generate this table.
In most other algorithms, a similar but less effective result can be obtained using a particular seed. Zedmee allows both.
| File input | #Values | #Expected Collisions | Collisions with Default table | Seeds table (genTable()) | Collisions |
|---|---|---|---|---|---|
| File first_million_primes.txt | 1,000,000 | 116 | 101 | 620231510, -1437367977, 1068537278, 1691867698 | 63 |
| File random_64bit_signed_numbers.txt | 1,000,000 | 116 | 101 | -1418137677, -1574389196, -738336105, -940565353 | 63 |
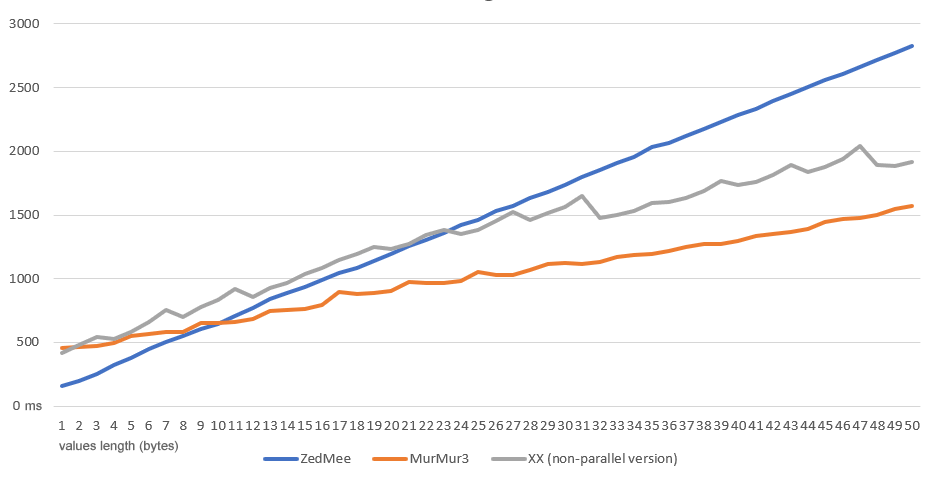
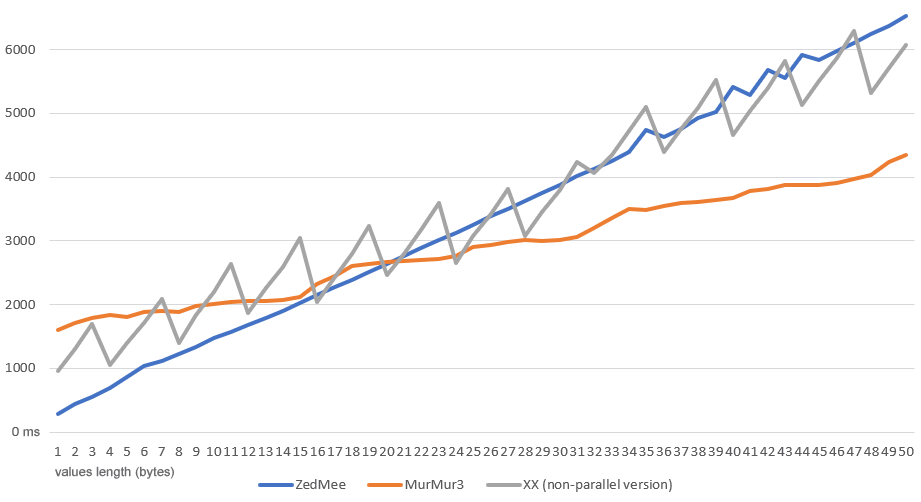
ZedMee is generally slower than the other two algorithms as they group the input bytes into blocks of 4 (or 8) and thus perform fewer operations, but they produce different results for x86 and x64 platforms
Zedmee, like most non-cryptographic functions, is non-secure because it is not specifically designed to be difficult to reverse by an adversary, making it unsuitable for cryptographic purposes. Its use is instead recommended in all other contexts where hash functions are used.
Like other non-cryptographic functions, its security depends on the secrecy of the possibly used seed, but unlike most other algorithms, zedmee allows you to use a 256 length table of 32-bit random values (or 64-bit for zedmee64) which make it much more secure than the others functions.
It is minimalist, elegant, straightforward and can be easily written in virtually any programming language. It produces the same result with x86 and x64 platforms. Currently C and Java versions are available.
Zedmee demonstrates to have an excellet quality of the dispersion, close to an ideal Universal Hash Function. It is simple, portable and produces same results in all platform. On the other hand it is slightly slower than XX and Murmur3. If the goal is the quality of the dispersion and have the same result on different platforms, ZedMee is certainly the algorithm to choose!