An API to automate parametric modeling with symbolic regression, originally developed for data analysis in the experimental high-energy physics community, but also applicable beyond.
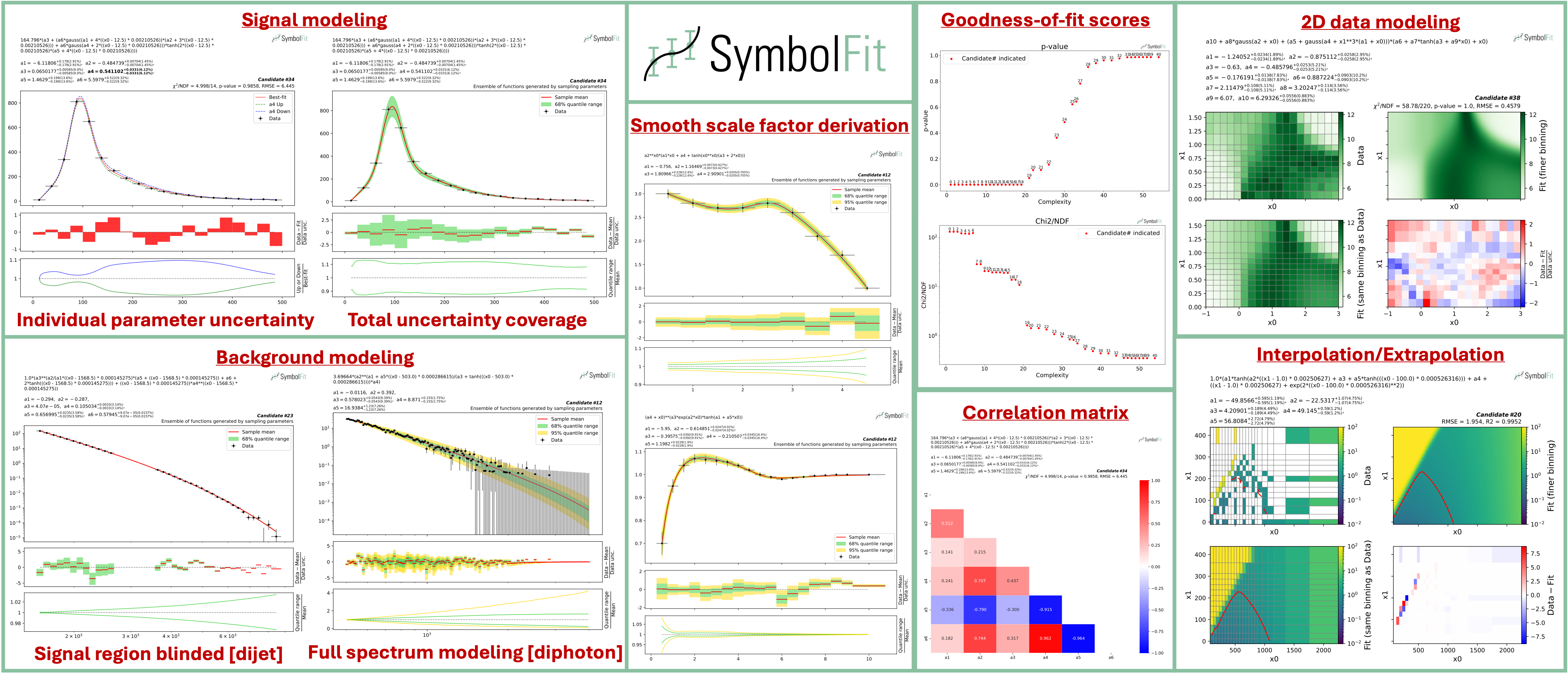
SymbolFit takes binned data with measurement/systematic uncertainties (optional) as input, utilizes PySR to perform a machine-search for batches of functional forms that model the data, parameterizes these functions, and utilizes LMFIT to re-optimize the functions and provide uncertainty estimation, all in one go. It is designed to maximize automation with minimal human input. Each run produces a batch of functions with uncertainty estimation, which are evaluated, saved, and plotted automatically into readable output files, ready for downstream tasks.
Note: This API is actively being updated to accommodate more use cases, so any feedback and contributions are very much welcomed and appreciated! If you encounter any problems while using it, please don’t hesitate to:
- Report bugs or suggest new features at
- Ask for specific help and recommendations for your dataset at
If you don't feel like sharing your data in public, please feel free to drop me a message or
. We are happy to assist in getting it to work on your data!
Prerequisite
Install Julia (backend for PySR):
curl -fsSL https://install.julialang.org | sh
Then check if installed properly:
julia --version
If julia is not found, most probably it is not yet included in PATH. To include, do:
export PATH="$PATH:/path/to/<Julia directory>/bin"
Check out here for platform-specific instructions.
Afterward, it is recommended to start from an empty virtual environment for installing and running SymbolFit.
‣ Installation via PyPI
With python>=3.9 and pip:
pip install symbolfit
‣ Installation via conda
conda create --name symbolfit_env python=3.9
conda activate symbolfit_env
conda install -c conda-forge symbolfit
‣ Editable installation for developers
git clone https://github.com/hftsoi/symbolfit.git
cd symbolfit
pip install -e .
To run an example fit, get the example datasets by cloning this repo:
git clone https://github.com/hftsoi/symbolfit.git
cd symbolfit
Then within a python session (or simply do python fit_example.py):
from symbolfit.symbolfit import *
dataset = importlib.import_module('examples.datasets.toy_dataset_1.dataset')
pysr_config = importlib.import_module('examples.pysr_configs.pysr_config_gauss').pysr_config
model = SymbolFit(
x = dataset.x,
y = dataset.y,
y_up = dataset.y_up,
y_down = dataset.y_down,
pysr_config = pysr_config,
max_complexity = 60,
input_rescale = True,
scale_y_by = 'mean',
max_stderr = 20,
fit_y_unc = True,
random_seed = None,
loss_weights = None
)
model.fit()
After the fit, save results to csv files:
model.save_to_csv(output_dir = 'output_dir/')
and plot results to pdf files:
model.plot_to_pdf(
output_dir = 'output_dir/',
bin_widths_1d = dataset.bin_widths_1d,
plot_logy = False,
plot_logx = False,
sampling_95quantile = False,
#bin_edges_2d = dataset.bin_edges_2d,
#plot_logx0 = False,
#plot_logx1 = False,
#cbar_min = None,
#cbar_max = None,
#cmap = None,
#contour = None,
# ^ additional options for 2D plotting
)
Candidate functions with full substitutions can be printed promptly:
model.print_candidate(candidate_number = 20)
When preparing for your own data, a graphical illustration of the input data format can be found here.
Each fit will produce a batch of candidate functions and will automatically save all results to six output files:
candidates.csv: saves all candidate functions and evaluations in a csv table.candidates_reduced.csv: saves a reduced version for essential information without intermediate results.candidates.pdf: plots all candidate functions (1D/2D only for now) with associated uncertainties one by one for fit quality evaluation.candidates_sampling.pdf: plots all candidate functions (1D only for now) with total uncertainty coverage generated by sampling parameters.candidates_gof.pdf: plots the goodness-of-fit scores.candidates_correlation.pdf: plots the correlation matrices for the parameters of the candidate functions.
Output files from an example fit can be found and downloaded here for illustration.
For detailed instructions and more demonstrations, please check out the Colab notebook and the documentation.
The documentation can be found here for more information and demonstrations.
If you find this useful in your research, please consider citing SymbolFit:
@misc{tsoi2024symbolfitautomaticparametricmodeling,
title = {{SymbolFit: Automatic Parametric Modeling with Symbolic Regression}},
author = {Ho Fung Tsoi and Dylan Rankin and Cecile Caillol and Miles Cranmer and Sridhara Dasu and Javier Duarte and Philip Harris and Elliot Lipeles and Vladimir Loncar},
year = {2024},
eprint = {2411.09851},
archivePrefix = {arXiv},
primaryClass = {hep-ex},
url = {https://arxiv.org/abs/2411.09851},
}
and PySR:
@misc{cranmerInterpretableMachineLearning2023,
title = {Interpretable {Machine} {Learning} for {Science} with {PySR} and {SymbolicRegression}.jl},
url = {http://arxiv.org/abs/2305.01582},
doi = {10.48550/arXiv.2305.01582},
urldate = {2023-07-17},
publisher = {arXiv},
author = {Cranmer, Miles},
month = may,
year = {2023},
note = {arXiv:2305.01582 [astro-ph, physics:physics]},
keywords = {Astrophysics - Instrumentation and Methods for Astrophysics, Computer Science - Machine Learning, Computer Science - Neural and Evolutionary Computing, Computer Science - Symbolic Computation, Physics - Data Analysis, Statistics and Probability},
}