lec1.Rmd

# Modelling spatio-temporal processes

## 1. Course overview, time series

### 1.1 Literature

* C. Chatfield, The analysis of time series: an introduction. Chapman and Hall: chapters 1, 2 and 3 
* Applied Spatial Data Analysis with R, by R. Bivand, E. Pebesma and V. Gomez-Rubio (Springer; 
[first edition](http://www.springer.com/978-0-387-78170-9) or its [second edition](http://www.springer.com/statistics/life+sciences%2C+medicine+%26+health/book/978-1-4614-7617-7)): 
 * Ch 1, 2, 3
 * Ch 4, 5
 * 1st ed, Ch 6 (customizing classes for spatial data) or 2nd ed, Ch 6 (spatio-temporal data)
 * Ch 8 (geostatistics)

### 1.2 Organization

Teachers:
 * Christoph Stasch (exercises)
 * Edzer Pebesma (lectures)

Learnweb:
 * subscribe! it's free!

Slides:
 * html on http://ifgi.uni-muenster.de/~epebe_01/mstp
 * Rmd sources on on http://github.com/edzer/mstp
 * you can run the Rmd files in rstudio (http://www.rstudio.com/)
 * pull requests with improvements are appreciated (and may be rewarded)

### 1.3 examen:
 * multiple choice, 4 possibilities, 40 questions, 20 need to be correct.

## 2. Where we come from

+ introduction to geostatistics
+ mathematics, linear algebra
+ computer science

### 2.1 geostatistics

+ types of variables: nominal, ordinal, interval, ratio
+ ... discrete, continuous
+ t-tests, ANOVA
+ regression, multiple regression (but now how we compute it)
+ assumption was: observations are independent
+ what does independence mean?

### 2.2 In this course
+ we will study dependence in observations, in 
 + space
 + time
 + or space-time
+ we will study how we can represent phenomena, by
 + mathematical representations (models)
 + computer representations (models)
+ we will consider how well these models correspond to our observations
 
## 3. Spatio-temporal phenomena are everywhere
+ if we think about it, there are no data that can be non-spatial or non-temporal.
+ in many cases, the spatial or temporal references are not essential
 + think: brain image of a person: time matters, spatial location of the MRI scanner not
 (hopefully!)
 + but: ID of the patient does!
 + and: time of scan matters too!
+ we will pigeon-hole phenomena into: fields, objects, aggregations

### 3.1 fields
+ many processes can be represented by fields, meaning they could be measured everywhere
+ think: temperature in this room
+ typical problems: interpolation, patterns, trends, temporal development, forecasting?

### 3.2 objects
+ objects can be identified (within a frame of observations)
+ between objects, there are no objects (no point of interpolation)
+ objects can be moving (people) static (buildings)

### 3.3 aggregations
+ we can aggregate fields, or objects, but do this differently:
+ population can be summed, temperature cannot

## 3.4 Aims of modelling
... could be
+ curiousity
+ studying models is easier than measuring the world around us
+ they mostly live in computers
+ there are so many different models
+ models really _use_ my CPU

Scientific aims of modelling are 

+ to learn about the world around us
+ to predict the past, current or future, in case where measurement is not feasible.

### 3.5 What is a model?
+ conceptual models (the water cycle: http://en.wikipedia.org/wiki/File:Water_cycle.png)
+ object models (e.g., UML: http://en.wikipedia.org/wiki/File:UML_diagrams_overview.svg)
+ mathematical models, such as Navier Stokes equation:

![Navier Stokes equation](http://upload.wikimedia.org/math/4/f/e/4fef570fa684173cbc6e70a904dd5e66.png)

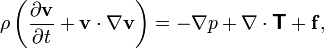
### 3.6 What is a mathematical model?
A mathematical model is an abstract model that uses mathematical
language to describe the behaviour of a system. 

> a representation of the essential aspects of an existing system (or
> a system to be constructed) which presents knowledge of that system in
> usable form (P. Eykhoff, 1974, System Identification, J. Wiley, London.)

In the natural sciences, a model is always an approximation, a
simplification of reality. If degree of approximation meets the required
accuracy, the model is useful, or valid (of value). A validated model
does not imply that the model is ``true''; more than one model can be
valid at the same time.

## 4. Time series models
we will first look into time series models, because they are
+ simple
+ easy to write down
+ well understood

time series models are roughly divided in 
1. time domain models and, which look at correlations and memory
2. frequency domain models, which focus on periodicities 

Spatial equivalents are mostly found in (a), although (b) has
spatial equivalences as well (e.g. wavelets).

### 4.1 some data

Consider the following process ($\Delta t$  = 1 min):

```{r fig.width=10, fig.height=5}
rm(list = ls()) # clean up old data
load("meteo.RData")
ls()
names(meteo)
plot(T.outside~date, meteo, type='l', ylab = parse(text = "Temperature ({}*degree* C)"), xlab = "date, 2007")
title("Outside temperature, Hauteville, FR")
```

### 4.2 Questions
+ how can we describe this process in statistical terms?
+ how can we model this process?
+ (how) can we predict future observations?

### 4.3 White noise, and AR($n$)
Perhaps the simplest time series model is _white noise_ with mean $m$:

$$y_t = m + e_t, \ \ e_t \sim N(0,\sigma^2)$$

$N(0,\sigma^2)$ denoting the normal distribution with mean 0 and
variance $\sigma^2$, and $\sim$ meaning _distributed as_ or _coming from_.

$t$ is the index $t=1,2,...,n$ of the observation, and refers to
specific times, which, when not otherwise specified are at regular
intervals.

A *white noise* process is completely without memory: each observation is
independent from its past or future. Plotting independent, standard normal
values against their index (the default for plotting a vector in R) shows
how a white noise time series would look like:

```{r fig.width=10, fig.height=5}
white.noise = rnorm(100)
plot(white.noise, type='b')
title("100 independent observations from N(0,1)")
```

```{r fig.width=10, fig.height=5}
white.noise = rnorm(1000)
plot(white.noise, type='l')
title("1000 independent observations from N(0,1)")
```

```{r fig.width=10, fig.height=5}
white.noise = rnorm(10000)
plot(white.noise, type='l')
title("10000 independent observations from N(0,1)")
```
We can look at the auto-correlation function of a white noise
process, and find it is uncorrelated for any lag larger than 0:

```{r fig.width=10, fig.height=5}
plot(acf(white.noise))
```

### 4.4 Autocorrelation
Autocorrelation (or lagged correlation) is the correlation between $y_i$ and $y_{i+h}$, as a function of the lag $h$:
$$
r(h) = \frac{\sum_{i=1}^{n-h}(y_i-\bar{y})(y_{i+h}-\bar{y})}{\sum_{i=1}^n (y_i-\bar{y})^2}
$$
with $\bar{y} = \frac{1}{n} \sum_{i=1}^n y_i$

### 4.5 Random walk
A simple, next model to look at is that of _random walk_, where each
time step a change is made according to a white noise process:
$$y_t = y_{t-1} + e_t$$
Such a process has memory, and long-range correlation. If we take the first-order
differences,
$$y_t - y_{t-1} = e_t$$
we obtain the white noise process.

Further, the variance of the process increases with increasing domain
(i.e., it is non-stationary)

### 4.6 Example random walk:
We can compute it as the cumulative sum of standard normal deviates: $y_n = \sum_{i=1}^n
e_i$:

```{r fig.width=10, fig.height=5}
# generate three series:
rw1 = cumsum(rnorm(5000))
rw2 = cumsum(rnorm(5000))
rw3 = cumsum(rnorm(5000))
plot(rw1, type='l', ylim = range(c(rw1,rw2,rw3)))
lines(rw2, type='l', col='red')
lines(rw3, type='l', col='blue')
```

```{r fig.width=10, fig.height=5}
plot(acf(rw3))
```

```{r fig.width=10, fig.height=5}
plot(acf(diff(rw3)))
```

### 4.7 MA(1), MA(q)
Let $e_t$ be a white noise process. A moving average process of
order $q$ is generated by
$$y_t = \beta_0 e_t + \beta_1 e_{t-1} + ... + \beta_q e_{t-q}$$

Note that the $\beta_j$ are weights, and could be $\frac{1}{q+1}$ to
obtain an unweighted average. Moving averaging smoothes the white
noise series $e_t$.

Moving average over monthly CO2 measurements on Maunaloa:
```{r fig.width=10, fig.height=5}
plot(co2)
lines(filter(co2, rep(1/12, 12)), col='blue')
```

Moving averages over a white noise process:
```{r fig.width=10, fig.height=5}
e = rnorm(200)
plot(e, type='l')
lines(filter(e, rep(1/5, 5)), col='red')
lines(filter(e, rep(1/20, 20)), col='blue')
```
Wider moving average filters give new processes with
+ less variation
+ stronger correlation, over larger lags

### 4.8 AR(1), AR(p)
An auto-regressive (1) model, or AR(1) model is generated by
$$y_t = \phi_1 y_{t-1}+e_t$$
and is sometimes called a Markov process. Given knowledge of $y_{t-1}$,
observations further back carry no information; more formally:
$$\Pr(y_t|y_{t-1},y_{t-2},...,y_{t-q}) = \Pr(y_t|y_{t-1})$$

+ $\phi_1 = 1$ gives random walk, $\phi_1=0$ gives white noise.
+ AR(1) processes have correlations beyond lag 1
+ AR(1) processes have non-significant _partial autocorrelations_ beyond lag 1

### 4.9 AR(p)
$$y_t = \phi_1 y_{t-1}+ \phi_2 y_{t-2} + ... + \phi_p y_{t-p} + e_t$$
or
$$y_t = \sum_{j=1}^p \phi_j y_{t-j}+e_t$$
+ The state of $y_t$ does not _only_ depend on $y_{t-1}$, but
observations further back contain information
+ AR(p) have autocorrelations beyond lag p
+ AR(p) have ``zero'' _partial_ autocorrelations beyond lag p

### 4.10 What is partial correlation?
+ Correlation between $y_t$ and $y_{t-2}$ is simply
obtained by plotting both series of length $n-2$, and computing 
correlation
+ Lag-2 _partial_ autocorrelation of $y_t$ and $y_{t-2}$, given
the value inbetween $y_{t-1}$ is obtained by
 + computing residuals $\hat{e}_t$ from regressing of $y_t$ on $y_{t-1}$
 + computing residuals $\hat{e}_{t-2}$ from regressing of $y_{t-2}$ on $y_{t-1}$
 + computing the correlation between both residual series $\hat{e}_t$ and
 $\hat{e}_{t-2}$.
+ Lag-3 partial autocorrelation regresses $y_t$ and $y_{t-3}$ 
on _both_ intermediate values $y_{t-1}$ and $y_{t-2}$
+ etc.

Partial correlation can help reveal what the order of an AR(p) series is.

### 4.11 relation between AR and MA processes
Chatwin has more details about this.  Substitute the AR(1) as follows
$$y_t = \phi_1 y_{t-1} + e_t$$
$$y_t = \phi_1 (\phi_1 y_{t-2} + e_{t-1}) + e_t$$
$$y_t = \phi_1^2 (\phi_1 y_{t-3} + e_{t-2}) + \phi_1 e_{t-1} + e_t$$
etc. In the limit, we can write any AR process as an (infinite)
MA process, and vice versa.