-
Notifications
You must be signed in to change notification settings - Fork 8
/
Copy pathindex.qmd
158 lines (120 loc) · 6.09 KB
/
index.qmd
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
# Course overview {.unnumbered}
## Literature
* C. Chatfield, The analysis of time series: an introduction. Chapman and Hall: chapters 1, 2 and 3 [@chatfield]
* R. Hyndman, G. Athanasopoulos: [Foreasting: Principles and Practice](https://otexts.com/fpp3/)
* Spatial Data Science, with applications in R [@sdsr]:
* Ch 1 (intro), 7 (sf, stars)
* Ch 12 (interpolation)
## Organization
Teachers:
* Christian Knoth (exercises, Wed 12-14)
* Edzer Pebesma (lectures)
Learnweb:
* subscribe
* no password
* Lectures + exercises is only one course.
Slides:
* rendered: [https://edzer.github.io/mstp/](https://edzer.github.io/mstp/)
* qmd (quarto) sources on on [http://github.com/edzer/mstp](http://github.com/edzer/mstp)
* you can load and run the individual qmd files in [rstudio](http://www.rstudio.com/)
* pull requests with improvements are appreciated (and may be rewarded):
* fork the repository on GitHub,
* click "Edit this page" on the right-hand-side
### Examen:
* multiple choice, 4 possibilities, 40 questions, 20 need to be correct.
### Overview of the course
Topics:
* Time series data
* Time series models: AR(p), MA(q), partial correlation, AIC, forecasting
* Optimisation:
* Linear models, least squares: normal equations
* Non-linear:
* One-dimensional: golden search
* Multi-dimensional least squares: Newton
* Multi-dimensional stochastic search: Metropolis
* Multi-dimensional stochastic optimisation: Metropolis
* Spatial models:
* Simple, heuristic spatial interpolation approaches
* Spatial correlation
* Regression with spatially correlated data
* Kriging: best linear (unbiased) prediction
* Stationarity, variogram
* Kriging varieties: simple, ordinary, universal kriging
* Kriging as a probabilistic spatial predictor
* Spatio-temporal variation modelled by partial differential equations
* Initial and boundary conditions
* Example
* Calibration: Kalman filter
## Where we come from
+ introduction to geostatistics
+ mathematics, linear algebra
+ computer science
### Introduction to geostatistics
+ types of variables: Stevens' measurement scales -- nominal, ordinal, interval, ratio
+ ... or: discrete, continuous
+ t-tests, ANOVA
+ regression, multiple regression (but not how we compute it)
+ assumption was: observations are _independent_
+ what does independence mean?
### In this course
+ we will study dependence in observations, in
+ space
+ time
+ or space-time
+ in space and/or time, Stevens' measurement scales are not enough! Examples:
+ linear time, cyclic time
+ space: functions, fields
+ we will study how we can represent phenomena, by
+ mathematical representations (models)
+ computer representations (models)
+ we will consider how well these models correspond to our observations
## Spatio-temporal phenomena are everywhere
+ if we think about it, there are no data that can be non-spatial or non-temporal.
+ in many cases, the spatial or temporal references are not essential
+ think: brain image of a person: time matters, but mostly referenced with respect to the age of the person, spatial location of the MRI scanner does not
+ but: ID of the patient does!
+ and: time of scan matters too!
+ we will "pigeon-hole" (classify) phenomena into: fields, objects, aggregations
### Fields
+ many processes can be represented by fields, meaning they could be measured everywhere
+ think: temperature in this room
+ typical problems: interpolation, patterns, trends, temporal development, forecasting?
### Objects and events
+ objects can be identified
+ objects are identified within a frame (or _window_) of observation
+ within this window, between objects, there are no objects (no point of interpolation)
+ objects can be moving (people), or static (buildings)
+ objects or events are sometimes obtained by thresholding fields, think heat wave, earthquake, hurricane, [see e.g.
@camara2014fields]
+ sometimes this view is rather artificial, think cars, persons, buildings
### Fields - objects/events conversions
+ we can convert a field into an object by thresholding (wind field, storm or hurricane)
+ we can convert objects into a field e.g. by computing the density as a continuous function
### Aggregations
+ we can aggregate fields, or objects, but do this differently:
+ population can be summed, temperature cannot (see [intensive/extensive properties](https://en.wikipedia.org/wiki/Intensive_and_extensive_properties))
## Aims of modelling
... could be
+ curiousity
+ fun: studying models is easier than measuring the world around us
More scientific aims of modelling are
+ to learn about the world around us
+ to predict the past, current or future, in case where measurement is not feasible.
### What is a model?
+ conceptual models, e.g. the water cycle ([wikipedia](http://en.wikipedia.org/wiki/File:Water_cycle.png):) 

+ object models, such as UML ([wikipedia](http://en.wikipedia.org/wiki/File:UML_diagrams_overview.svg):) 
+ mathematical models, such as Navier Stokes' equation, ([wikipedia](https://en.wikipedia.org/wiki/Navier%E2%80%93Stokes_equations):)
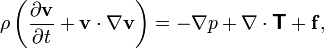
### What is a mathematical model?
A mathematical model is an abstract model that uses mathematical
language to describe the behaviour of a system, quoting [@eykhoff]
a mathematical model is:
> a representation of the essential aspects of an existing system (or
> a system to be constructed) which presents knowledge of that system in
> usable form
In the natural sciences, a model is always an approximation, a
simplification of reality. If degree of approximation meets the required
accuracy, the model is useful, or valid (of value). A validated model
does not imply that the model is "true"; more than one model can be
valid at the same time.