https://leetcode-cn.com/problems/max-black-square-lcci/
给定一个方阵,其中每个单元(像素)非黑即白。设计一个算法,找出 4 条边皆为黑色像素的最大子方阵。
返回一个数组 [r, c, size] ,其中 r, c 分别代表子方阵左上角的行号和列号,size 是子方阵的边长。若有多个满足条件的子方阵,返回 r 最小的,若 r 相同,返回 c 最小的子方阵。若无满足条件的子方阵,返回空数组。
示例 1:
输入:
[
[1,0,1],
[0,0,1],
[0,0,1]
]
输出: [1,0,2]
解释: 输入中 0 代表黑色,1 代表白色,标粗的元素即为满足条件的最大子方阵
示例 2:
输入:
[
[0,1,1],
[1,0,1],
[1,1,0]
]
输出: [0,0,1]
提示:
matrix.length == matrix[0].length <= 200
- 暂无
看了下数据范围,矩阵大小不超过
乍一看,这道题和 221. 最大正方形,实则不然。 这道题是可以空心的,只要边长是部分都是 0 即可,这就完全不同了。
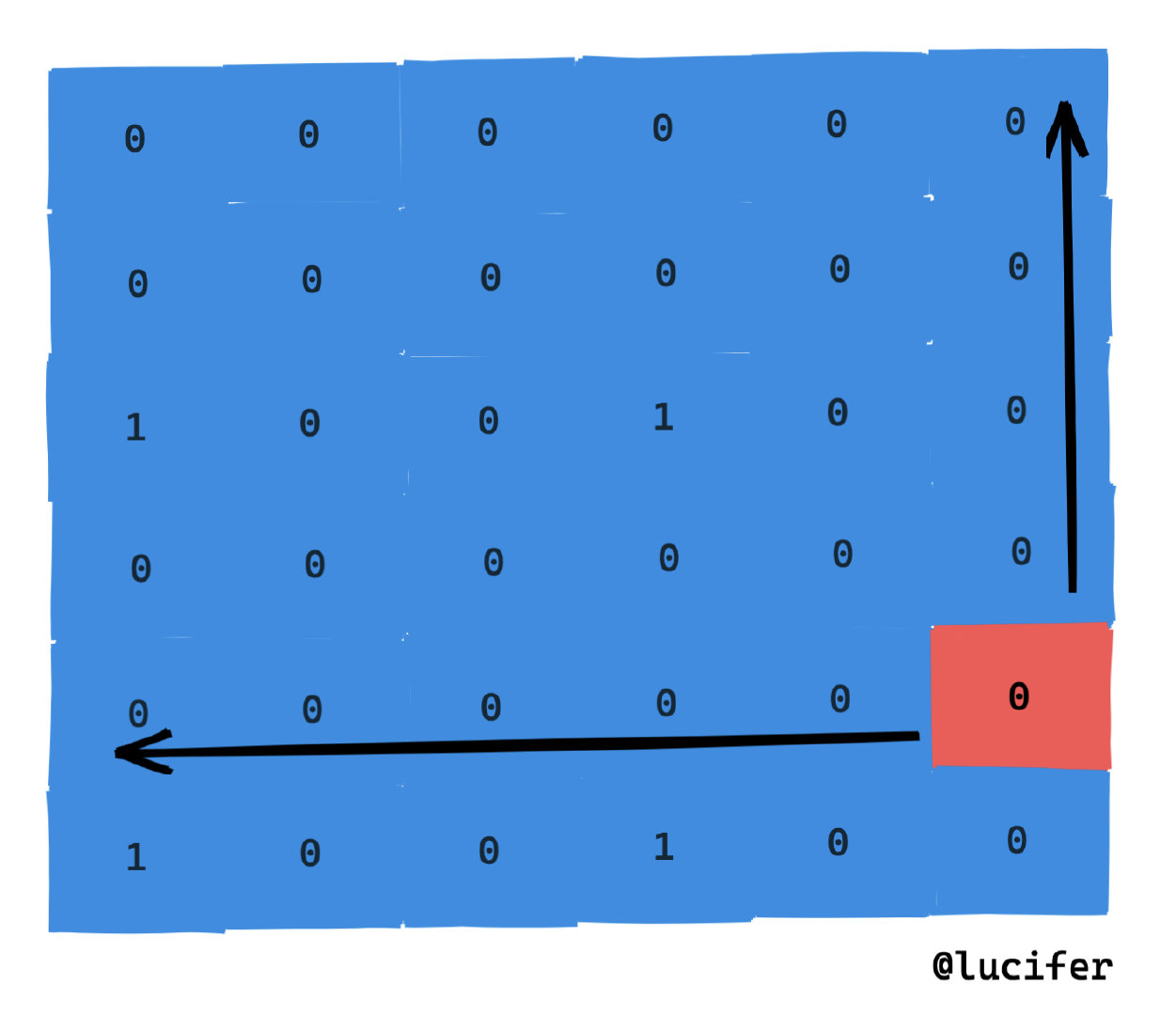
如下图,红色部分就是答案。只需要保证边全部是 0 就好了,所以里面有一个 1 无所谓的。
我们不妨从局部入手,看能不能打开思路。
这是一种常用的技巧,当你面对难题无从下手的时候可以画个图,从特殊情况和局部情况开始,帮助我们打开思路。
比如我想计算以如下图红色格子为右下角的最大黑方阵。我们可以从当前点向上向左扩展直到非 0。
在上面的例子中,不难看出其最大黑方阵不会超过 min(4, 5)。
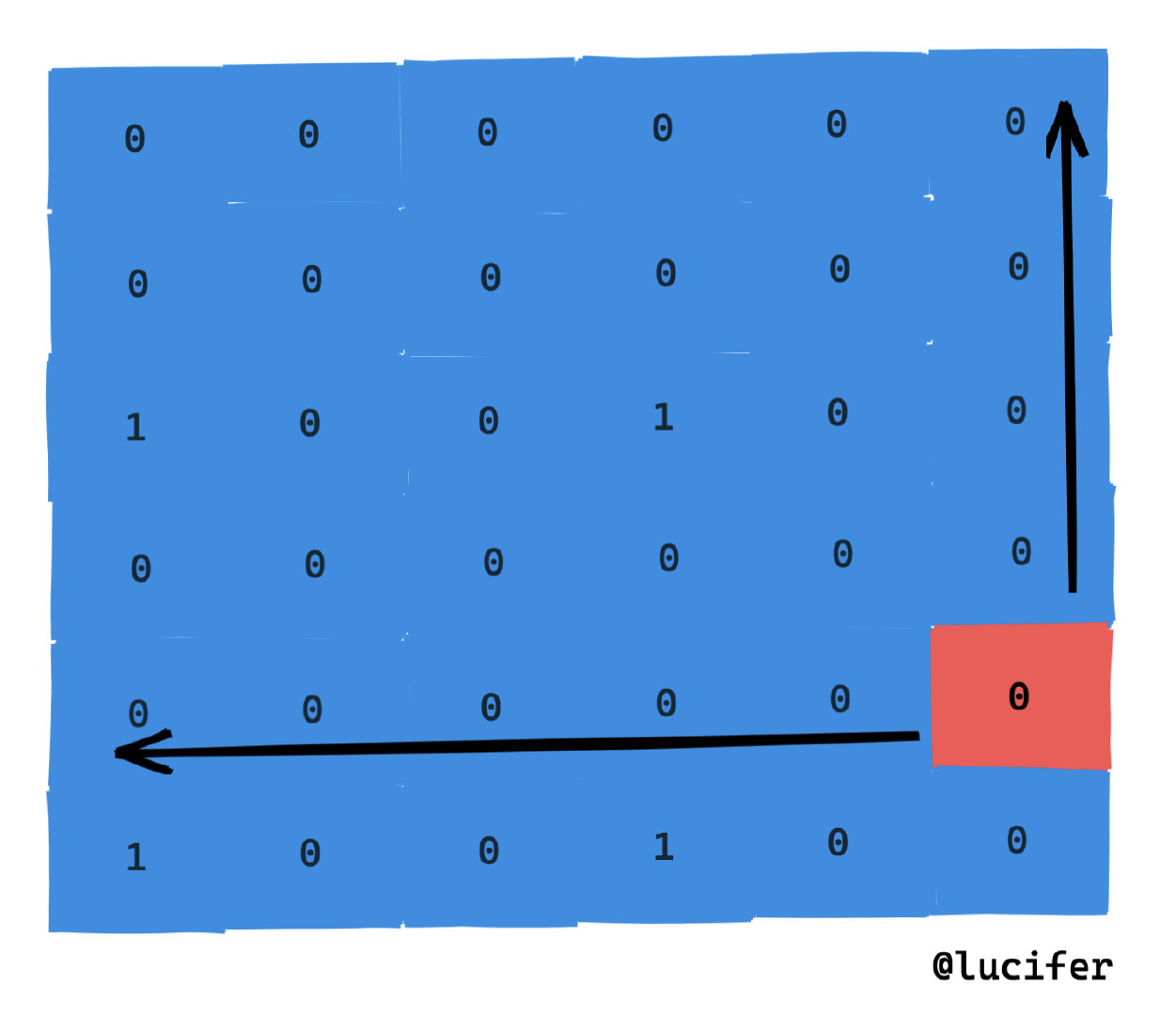
那答案直接就是 4 么? 对于这种情况是的, 但是也存在其他情况。比如:
因此解空间上界虽然是 4,但是下界仍然可能为 1。
下界为 1 是因为我们只对值为 0 的格子感兴趣,如果格子为 0 ,最差最大方阵就是自身。
上面我已经将算法锁定为暴力求解了。对于解空间的暴力求解怎么做?无非就是枚举所有解空间,最多减减枝。
直白一点来说就是:
- 1 可以么?
- 2 可以么?
- 3 可以么?
- 4 可以么?
这叫做特殊。
如果你已经搞懂了这个特殊情况, 那么一般情况也就不难了。
算法描述:
- 从左到右从上到下扫描一次矩阵。
- 如果格子值是 0,则分别向上和向左扫描直到第一个不是 0 的格子,那么最大方阵的上界就是 min(向左延伸的长度, 向上延伸的长度)。
- 逐步尝试[1, 上界] 直到无法形成方阵,最后可行的方阵就是以当前点能 形成的最大方阵。
- 扫描过程维护最大值,最后返回最大值以及顶点信息即可。
现在的难点只剩下第三点部分如何逐步尝试[1, 上界]。实际上这个也不难,只需要:
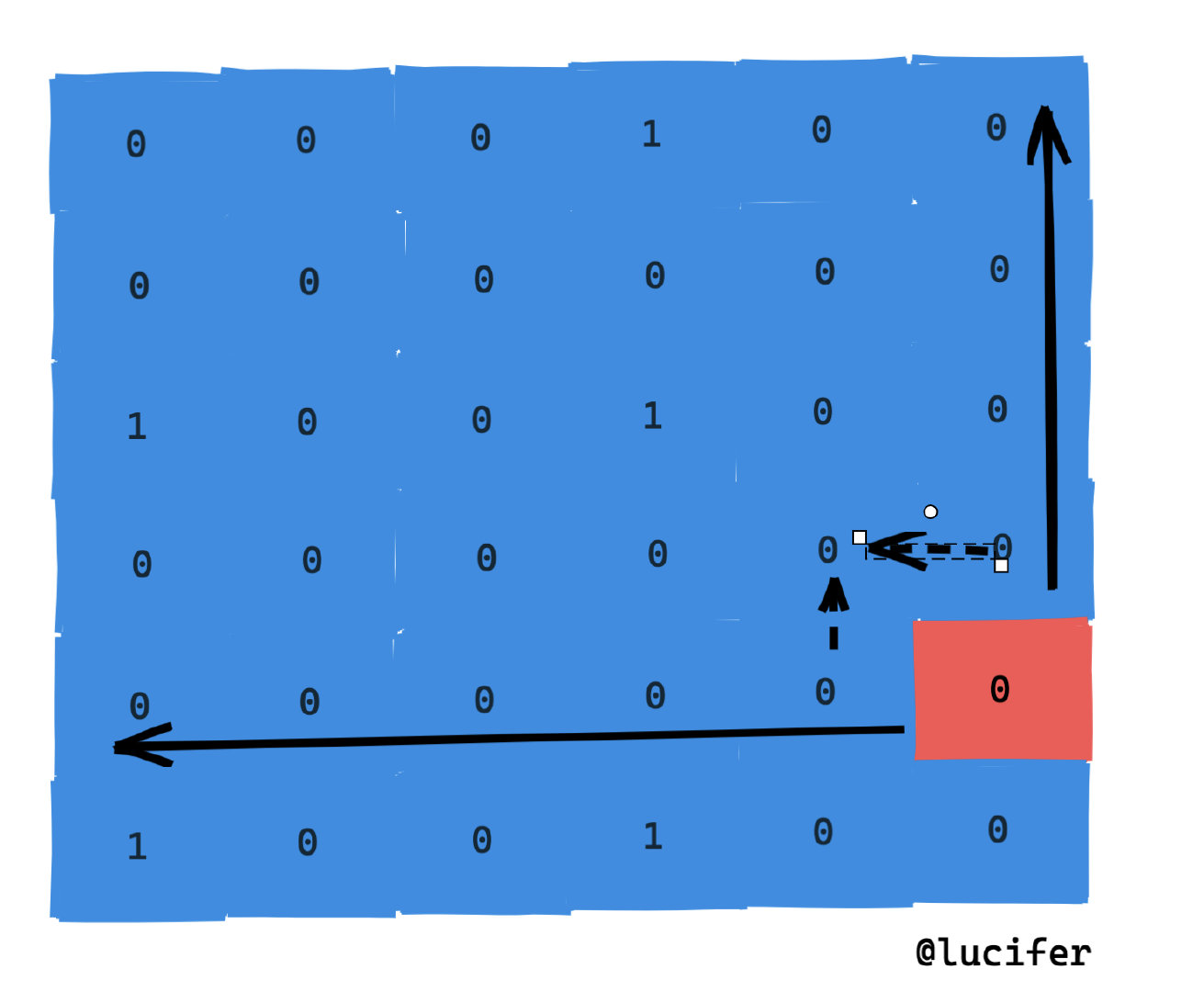
- 在向左延伸的同时向上探测
- 在向上延伸的同时向左探测
看一下图或许好理解一点。
如上图就是尝试 2 是否可行,如果可行,我们继续得寸进尺,直到不可行或者到上界。
接下来,分析一下算法的时间复杂度。
- 由于每一个为 0 的点都需要向左向上探测,那么最坏就是 O(N),其中 N 为边长。
- 向左向上的同时需要继续探测,这个复杂度最坏的情况也是 O(N)。
由于我们需要对最多$O(N^2)$个点执行上面的逻辑,因此总的时间复杂度就是
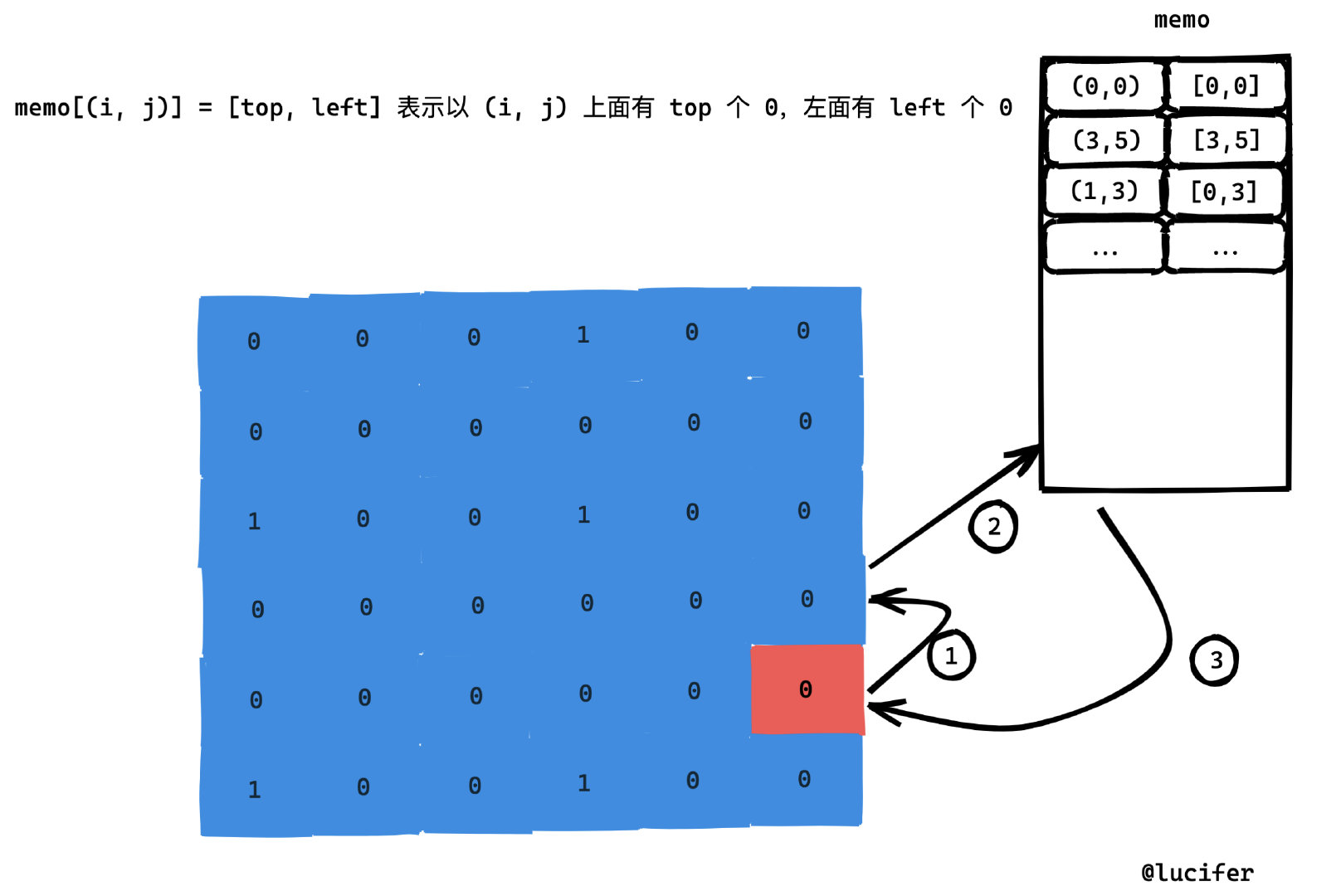
而实际上每一个格子都是一个独立的子问题, 因此可以使用一个 memo(比如哈希表)将每个格子的扩展结果保存起来,这样可以将复杂度优化到
比如上面提到的向上向左探测的过程,如果上面和左面格子的扩展结果已经计算出来了,那么直接用就行了,这部分延伸的复杂度可以降低到
- (4,5) 找到上方相邻的格子,如果是 1 直接返回。
- 如果上方格子值是 0 ,去 memo 中查询。
- memo 返回 结果,我们只需要将这个结果 + 1 就是可以向上延伸的最大长度了。
比如现在要计算以坐标(4,5) 为右下角的最大方阵的边长。第一步要向上探测到 (3,5),到达(3,5) 之后无需继续往上延伸而是从 memo 中获取。(4,5) 上方的 0 的格子就是(3,5) 上方的格子个数 + 1。
最后一个问题。什么数据结构可以实现上面查询过程
- 使用哈希 map 的好处是无非事先开辟空间。缺点是如果数据量太大,可能会因为哈希表的冲突处理导致超时。比如石子游戏使用哈希表存就很容易超时。
- 使用数组好处和坏处几乎和哈希表是相反的。数组需要实现指定大小, 但是数组是不会冲突的,也不需要计算哈希键,因此在很多情况下性能更好。进一步使用数组这种内存连续的数据结构对 CPU 友好,因此同样复杂度会更快。 而哈希表使用了链表或者树,因此对 CPU 缓存就没那么友好了。
综上,我推荐大家使用数组来存储。
这道题差不多就是这样了。实际上,这就是动态规划优化,其实也没什么神奇嘛,很多时候都是暴力枚举 + 记忆化而已。
代码支持:Java,Python
Java Code:
class Solution {
public int[] findSquare(int[][] matrix) {
int [] res = new int [0];
int [][][] dp = new int [2][matrix.length+1][matrix[0].length+1];
int max = 0
for(int i=1;i<=matrix.length;i++){
for(int j=1;j<=matrix[0].length;j++){
if(matrix[i-1][j-1]==0){
dp[0][i][j] = dp[0][i-1][j]+1;
dp[1][i][j] = dp[1][i][j-1]+1;
int bound = Math.min(dp[0][i][j], dp[1][i][j]);
for(int k=0;k<bound;k++){
if(dp[1][i-k][j]>=k+1&&dp[0][i][j-k]>=k+1){
if(k+1>max){
res = new int [3];
max = k+1;
res[0] = i-k-1;
res[1] = j-k-1;
res[2] = max;
}
}
}
}
}
}
return res;
}
}Python Code:
class Solution:
def findSquare(self, matrix: List[List[int]]) -> List[int]:
n = len(matrix)
dp = [[[0, 0] for _ in range(n + 1)] for _ in range(n + 1)]
ans = []
for i in range(1, n + 1):
for j in range(1, n + 1):
if matrix[i - 1][j - 1] == 0:
dp[i][j][0] = dp[i-1][j][0] + 1
dp[i][j][1] = dp[i][j-1][1] + 1
upper = min(dp[i][j][0], dp[i][j][1])
for k in range(upper):
if min(dp[i-k][j][1], dp[i][j-k][0]) >= k + 1:
if not ans or k + 1 > ans[2]:
ans = [i-k-1, j-k-1, k + 1]
return ans复杂度分析
- 时间复杂度:$O(N^3)$,其中 N 为矩阵边长。
- 空间复杂度:空间的瓶颈在于 memo,而 memo 的大小为矩阵的大小,因此空间复杂度为
$O(N^2)$ ,其中 N 为矩阵边长。
以上就是本文的全部内容了。大家对此有何看法,欢迎给我留言,我有时间都会一一查看回答。更多算法套路可以访问我的 LeetCode 题解仓库:https://github.com/azl397985856/leetcode 。 目前已经 38K star 啦。大家也可以关注我的公众号《力扣加加》带你啃下算法这块硬骨头。