Skip to content

Latest commit

 

History

History
380 lines (293 loc) · 11.7 KB

4.median-of-two-sorted-arrays.md

File metadata and controls

380 lines (293 loc) · 11.7 KB
Raw

题目地址(4. 寻找两个正序数组的中位数)

https://leetcode-cn.com/problems/median-of-two-sorted-arrays/

题目描述

给定两个大小为 m 和 n 的正序（从小到大）数组 nums1 和 nums2。

请你找出这两个正序数组的中位数，并且要求算法的时间复杂度为 O(log(m + n))。

你可以假设 nums1 和 nums2 不会同时为空。

 

示例 1:

nums1 = [1, 3]
nums2 = [2]

则中位数是 2.0
示例 2:

nums1 = [1, 2]
nums2 = [3, 4]

则中位数是 (2 + 3)/2 = 2.5

前置知识

  • 中位数
  • 分治法
  • 二分查找

公司

  • 阿里
  • 百度
  • 腾讯

暴力法

思路

首先了解一下 Median 的概念，一个数组中 median 就是把数组分成左右等分的中位数。

如下图：

中位数概念

知道了概念，我们先来看下如何使用暴力法来解决。

试了一下，暴力解法也是可以被 Leetcode Accept 的。

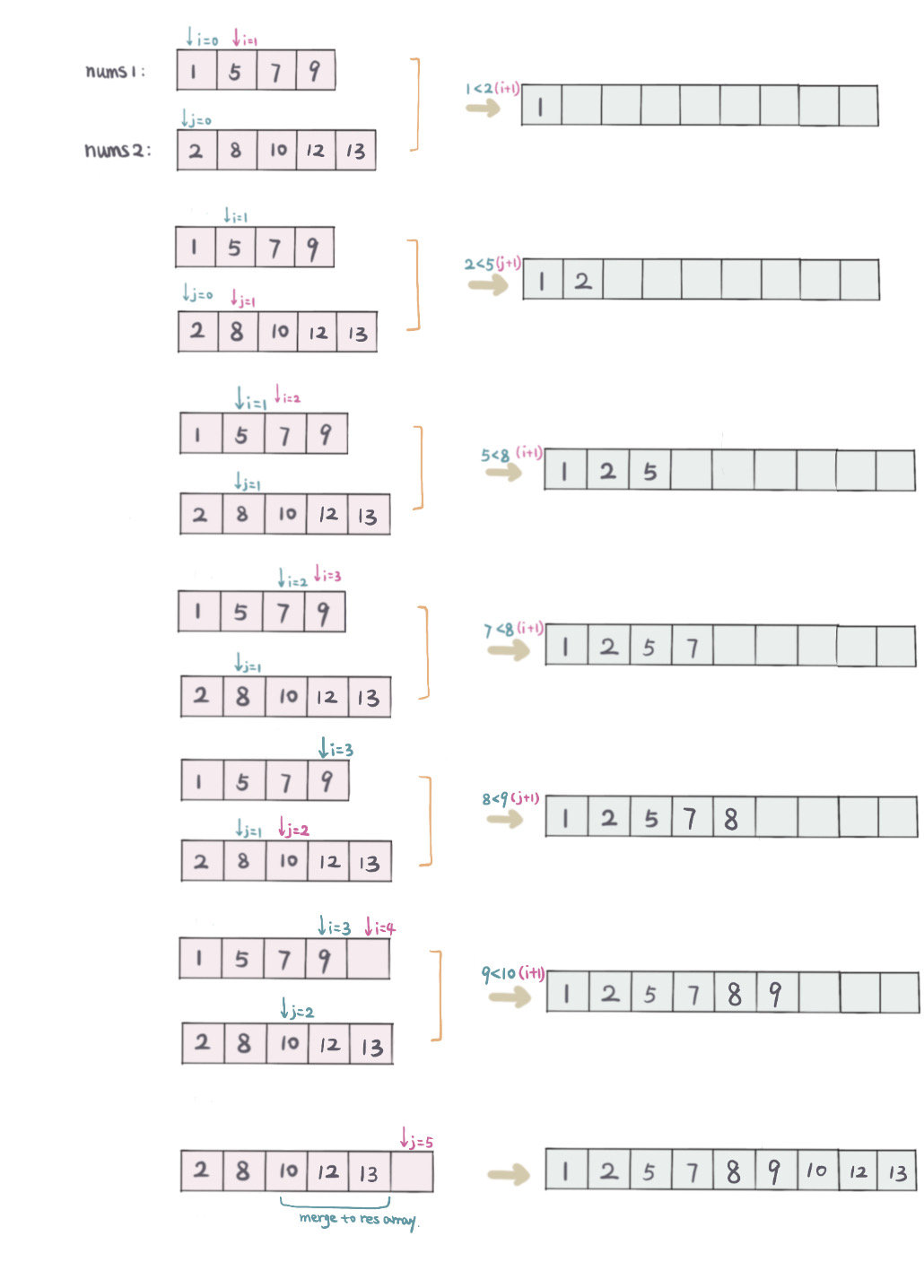
暴力解主要是要 merge 两个排序的数组（A，B）成一个排序的数组。

用两个pointer（i，j），i 从数组A起始位置开始，即i=0开始，j 从数组B起始位置， 即j=0开始. 一一比较 A[i] 和 B[j],

  1. 如果A[i] <= B[j], 则把A[i] 放入新的数组中，i 往后移一位，即 i+1.
  2. 如果A[i] > B[j], 则把B[j] 放入新的数组中，j 往后移一位，即 j+1.
  3. 重复步骤#1 和 #2，直到i移到A最后，或者j移到B最后。
  4. 如果j移动到B数组最后，那么直接把剩下的所有A依次放入新的数组中.
  5. 如果i移动到A数组最后，那么直接把剩下的所有B依次放入新的数组中.

整个过程类似归并排序的合并过程

Merge 的过程如下图。 暴力法图解

时间复杂度和空间复杂度都是O(m+n), 不符合题中给出O(log(m+n))时间复杂度的要求。

代码

代码支持： Java，JS：

Java Code：

class MedianTwoSortedArrayBruteForce {
    public double findMedianSortedArrays(int[] nums1, int[] nums2) {
      int[] newArr = mergeTwoSortedArray(nums1, nums2);
      int n = newArr.length;
      if (n % 2 == 0) {
        // even
        return (double) (newArr[n / 2] + newArr[n / 2 - 1]) / 2;
      } else {
        // odd
        return (double) newArr[n / 2];
      }
    }
    private int[] mergeTwoSortedArray(int[] nums1, int[] nums2) {
      int m = nums1.length;
      int n = nums2.length;
      int[] res = new int[m + n];
      int i = 0;
      int j = 0;
      int idx = 0;
      while (i < m && j < n) {
        if (nums1[i] <= nums2[j]) {
          res[idx++] = nums1[i++];
        } else {
          res[idx++] = nums2[j++];
        }
      }
      while (i < m) {
        res[idx++] = nums1[i++];
      }
      while (j < n) {
        res[idx++] = nums2[j++];
      }
      return res;
    }
}

JS Code:

/**
 * @param {number[]} nums1
 * @param {number[]} nums2
 * @return {number}
 */
var findMedianSortedArrays = function (nums1, nums2) {
  // 归并排序
  const merged = [];
  let i = 0;
  let j = 0;
  while (i < nums1.length && j < nums2.length) {
    if (nums1[i] < nums2[j]) {
      merged.push(nums1[i++]);
    } else {
      merged.push(nums2[j++]);
    }
  }
  while (i < nums1.length) {
    merged.push(nums1[i++]);
  }
  while (j < nums2.length) {
    merged.push(nums2[j++]);
  }

  const { length } = merged;
  return length % 2 === 1
    ? merged[Math.floor(length / 2)]
    : (merged[length / 2] + merged[length / 2 - 1]) / 2;
};

复杂度分析

  • 时间复杂度：$O(max(m, n))$
  • 空间复杂度：$O(m + n)$

二分查找

思路

如果我们把上一种方法的最终结果拿出来单独看的话，不难发现最终结果就是 nums1 和 nums 两个数组交错形成的新数组，也就是说 nums1 和 nums2 的相对位置并不会发生变化，这是本题的关键信息之一。

为了方便描述，不妨假设最终分割后，数组 nums1 左侧部分是 A，数组 nums2 左侧部分是 B。由于题中给出的数组都是排好序的，在排好序的数组中查找很容易想到可以用二分查找（Binary Search)·, 这里对数组长度小的做二分以减少时间复杂度。对较小的数组做二分可行的原因在于如果一个数组的索引 i 确定了，那么另一个数组的索引位置 j 也是确定的，因为 (i+1) + (j+1) 等于 (m + n + 1) / 2，其中 m 是数组 A 的长度， n 是数组 B 的长度。具体来说，我们可以保证数组 A 和 数组 B 做 partition 之后，len(Aleft)+len(Bleft)=(m+n+1)/2

接下来需要特别注意四个指针：leftp1, rightp1, leftp2, rightp2，分别表示 A 数组分割点，A 数组分割点右侧数，B 数组分割点，B 数组分割点右侧数。不过这里有两个临界点需要特殊处理：

  • 如果分割点左侧没有数，即分割点索引是 0，那么其左侧应该设置为无限小。
  • 如果分割点右侧没有数，即分割点索引是数组长度-1，那么其左侧应该设置为无限大。

如果我们二分之后满足：leftp1 < rightp2 and leftp2 < rightp1,那么说明分割是正确的，直接返回max(leftp1, leftp2)+min(rightp1, rightp2) 即可。否则，说明分割无效，我们需要调整分割点。

如何调整呢？实际上只需要判断 leftp1 > rightp2 的大小关系即可。如果 leftp1 > rightp2，那么说明 leftp1 太大了，我们可以通过缩小上界来降低 leftp1，否则我们需要扩大下界。

核心代码：

if leftp1 > rightp2:
    hi = mid1 - 1
else:
    lo = mid1 + 1

上面的调整上下界的代码是建立在对数组 nums1 进行二分的基础上的，如果我们对数组 nums2 进行二分，那么相应地需要改为：

if leftp2 > rightp1:
    hi = mid2 - 1
else:
    lo = mid2 + 1

下面我们通过一个具体的例子来说明。

比如对数组 A 的做 partition 的位置是区间[0,m]

如图： 详细算法图解

下图给出几种不同情况的例子（注意但左边或者右边没有元素的时候，左边用INF_MIN，右边用INF_MAX表示左右的元素：

实例解析

下图给出具体做的 partition 解题的例子步骤，

更详细的实例解析

这个算法关键在于：

  1. 要 partition 两个排好序的数组成左右两等份，partition 需要满足len(Aleft)+len(Bleft)=(m+n+1)/2 - m是数组A的长度， n是数组B的长度，
  2. 且 partition 后 A 左边最大(maxLeftA), A 右边最小（minRightA), B 左边最大（maxLeftB), B 右边最小（minRightB) 满足 (maxLeftA <= minRightB && maxLeftB <= minRightA)

关键点分析

  • 有序数组容易想到二分查找
  • 对小的数组进行二分可降低时间复杂度
  • 根据 leftp1,rightp2,leftp2 和 rightp1 的大小关系确定结束点和收缩方向

代码

代码支持：JS，CPP， Python3，

JS Code:

/**
 * 二分解法
 * @param {number[]} nums1
 * @param {number[]} nums2
 * @return {number}
 */
var findMedianSortedArrays = function (nums1, nums2) {
  // make sure to do binary search for shorten array
  if (nums1.length > nums2.length) {
    [nums1, nums2] = [nums2, nums1];
  }
  const m = nums1.length;
  const n = nums2.length;
  let low = 0;
  let high = m;
  while (low <= high) {
    const i = low + Math.floor((high - low) / 2);
    const j = Math.floor((m + n + 1) / 2) - i;

    const maxLeftA = i === 0 ? -Infinity : nums1[i - 1];
    const minRightA = i === m ? Infinity : nums1[i];
    const maxLeftB = j === 0 ? -Infinity : nums2[j - 1];
    const minRightB = j === n ? Infinity : nums2[j];

    if (maxLeftA <= minRightB && minRightA >= maxLeftB) {
      return (m + n) % 2 === 1
        ? Math.max(maxLeftA, maxLeftB)
        : (Math.max(maxLeftA, maxLeftB) + Math.min(minRightA, minRightB)) / 2;
    } else if (maxLeftA > minRightB) {
      high = i - 1;
    } else {
      low = low + 1;
    }
  }
};

Java Code:

class MedianSortedTwoArrayBinarySearch {
  public static double findMedianSortedArraysBinarySearch(int[] nums1, int[] nums2) {
     // do binary search for shorter length array, make sure time complexity log(min(m,n)).
     if (nums1.length > nums2.length) {
        return findMedianSortedArraysBinarySearch(nums2, nums1);
      }
      int m = nums1.length;
      int n = nums2.length;
      int lo = 0;
      int hi = m;
      while (lo <= hi) {
        // partition A position i
        int i = lo + (hi - lo) / 2;
        // partition B position j
        int j = (m + n + 1) / 2 - i;

        int maxLeftA = i == 0 ? Integer.MIN_VALUE : nums1[i - 1];
        int minRightA = i == m ? Integer.MAX_VALUE : nums1[i];

        int maxLeftB = j == 0 ? Integer.MIN_VALUE : nums2[j - 1];
        int minRightB = j == n ? Integer.MAX_VALUE : nums2[j];

        if (maxLeftA <= minRightB && maxLeftB <= minRightA) {
          // total length is even
          if ((m + n) % 2 == 0) {
            return (double) (Math.max(maxLeftA, maxLeftB) + Math.min(minRightA, minRightB)) / 2;
          } else {
            // total length is odd
            return (double) Math.max(maxLeftA, maxLeftB);
          }
        } else if (maxLeftA > minRightB) {
          // binary search left half
          hi = i - 1;
        } else {
          // binary search right half
          lo = i + 1;
        }
      }
      return 0.0;
    }
}

CPP Code:

class Solution {
public:
    double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
        if (nums1.size() > nums2.size()) swap(nums1, nums2);
        int M = nums1.size(), N = nums2.size(), L = 0, R = M, K = (M + N + 1) / 2;
        while (true) {
            int i = (L + R) / 2, j = K - i;
            if (i < M && nums2[j - 1] > nums1[i]) L = i + 1;
            else if (i > L && nums1[i - 1] > nums2[j]) R = i - 1;
            else {
                int maxLeft = max(i ? nums1[i - 1] : INT_MIN, j ? nums2[j - 1] : INT_MIN);
                if ((M + N) % 2) return maxLeft;
                int minRight = min(i == M ? INT_MAX : nums1[i], j == N ? INT_MAX : nums2[j]);
                return (maxLeft + minRight) / 2.0;
            }
        }
    }
};

Python3 Code:

class Solution:
    def findMedianSortedArrays(self, nums1: List[int], nums2: List[int]) -> float:
        N = len(nums1)
        M = len(nums2)
        if N > M:
            return self.findMedianSortedArrays(nums2, nums1)

        lo = 0
        hi = N
        combined = N + M

        while lo <= hi:
            mid1 = lo + hi >> 1
            mid2 = ((combined + 1) >> 1) - mid1

            leftp1 = -float("inf") if mid1 == 0 else nums1[mid1 - 1]
            rightp1 = float("inf") if mid1 == N else nums1[mid1]

            leftp2 = -float("inf") if mid2 == 0 else nums2[mid2 - 1]
            rightp2 = float("inf") if mid2 == M else nums2[mid2]

            # Check if the partition is valid for the case of
            if leftp1 <= rightp2 and leftp2 <= rightp1:
                if combined % 2 == 0:
                    return (max(leftp1, leftp2)+min(rightp1, rightp2)) / 2.0

                return max(leftp1, leftp2)
            else:
                if leftp1 > rightp2:
                    hi = mid1 - 1
                else:
                    lo = mid1 + 1
        return -1

复杂度分析

  • 时间复杂度：$O(log(min(m, n)))$
  • 空间复杂度：$O(log(min(m, n)))$

大家对此有何看法，欢迎给我留言，我有时间都会一一查看回答。更多算法套路可以访问我的 LeetCode 题解仓库：https://github.com/azl397985856/leetcode 。 目前已经 40K star 啦。 大家也可以关注我的公众号《力扣加加》带你啃下算法这块硬骨头。